Altres
SDG
Per consultar les dades del SDG Index amb R, descarregarem les dades i les situarem al directori de treball, tal com hem vist anteriorment a la Guia d’RStudio. Haurem de tenir carregats els paquets readxl i dplyr.
library(dplyr)
library(readxl)
sdg <- read_xlsx("SDR 2021 - Database.xlsx", sheet = 4)Si visualitzem les dades de l’objecte sdg, veurem que tenim 193 observacions (és a dir, 193 països) i 125 variables.
sdg
## # A tibble: 193 × 125
## Country Cod…¹ Country Regio…² Popul…³ Pover…⁴ Pover…⁵ Pover…⁶ Preva…⁷ Preva…⁸
## <chr> <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 AFG Afghan… E. Eur… 3.89e7 NA NA NA 29.9 38.2
## 2 ALB Albania E. Eur… 2.88e6 0.16 8.5 NA 3.6 11.3
## 3 DZA Algeria MENA 4.39e7 0.37 2.89 NA 2.8 11.7
## 4 AND Andorra E. Eur… 7.73e4 NA NA NA 1.17 2.58
## 5 AGO Angola Africa 3.29e7 53.8 75.7 NA 18.6 37.6
## 6 ATG Antigu… LAC 9.79e4 NA NA NA 1.17 2.58
## 7 ARG Argent… LAC 4.52e7 0.86 3.52 NA 3.8 7.9
## 8 ARM Armenia E. Eur… 2.96e6 0.83 6.17 NA 2.6 9.4
## 9 AUS Austra… OECD 2.55e7 0.2 0.26 12.4 2.5 2
## 10 AUT Austria OECD 9.01e6 0.28 0.35 9.4 2.5 2.58
## # … with 183 more rows, 116 more variables:
## # `Prevalence of wasting in children under 5 years of age (%)` <dbl>,
## # `Prevalence of obesity, BMI ≥ 30 (% of adult population)` <dbl>,
## # `Human Trophic Level (best 2-3 worst)` <dbl>,
## # `Cereal yield (tonnes per hectare of harvested land)` <dbl>,
## # `Sustainable Nitrogen Management Index (best 0-1.41 worst)` <dbl>,
## # `Yield gap closure (% of potential yield)` <dbl>, …Per visualitzar-les millor, recomanem utilitzar glimpse()
glimpse(sdg)Si ens interessa algun indicador concret, podem observar algunes de les seves característiques com:
- La mitjana:
mean(). - El valor màxim
max(). - El valor mínim
min().
Per exemple:
mean(sdg$`Poverty headcount ratio at $1.90/day (%)`, na.rm = T)
## [1] 13.35112Si volem incloure una taula que resumeixi els indicadors, ho podem fer així:
- Posem cada indicador a dins de
select(), separats per comes. - Cada indicador el posem en aquest format:
`nom_curt = `Nom llarg` - Amb
head(10), demanem només les 10 primeres observacions.
sdg |>
select(Country,
pop = `Population in 2020`,
htl = `Human Trophic Level (best 2-3 worst)`,
traffic = `Traffic deaths (per 100,000 population)`) |>
head(10) |>
knitr::kable()| Country | pop | htl | traffic |
|---|---|---|---|
| Afghanistan | 38928341 | 2.190 | 15.86 |
| Albania | 2877800 | 2.383 | 11.70 |
| Algeria | 43851043 | 2.199 | 20.90 |
| Andorra | 77265 | NA | NA |
| Angola | 32866268 | 2.131 | 26.13 |
| Antigua and Barbuda | 97928 | 2.418 | 0.00 |
| Argentina | 45195777 | 2.405 | 14.06 |
| Armenia | 2963234 | 2.280 | 19.95 |
| Australia | 25499881 | 2.468 | 4.94 |
| Austria | 9006400 | 2.412 | 4.87 |
En aquest cas, incloeu un petit llibre de codis que indiqui què és cara variable. Simplement, amb posar què equival cada variable n’hi ha prou. Exemple:
- Pop: Population in 2020`
- HTL: Human Trophic Level (best 2-3 worst)
- Traffic: Traffic deaths (per 100,000 population)
PIB
Identifica tots els problemes entre concepte i mesurament d’aquest tuit.
Carai com perjudiquen l'economia els governs d'esquerres llatinoamericans... #Bolívia pic.twitter.com/mDwI2IF6ep
— Roger Tugas Vilardell 📊 (@rogertugas) October 20, 2020
Mai fins ara s’havien destinat tants recursos públics en educació. Mai! pic.twitter.com/299f2Ce6gz
— Oriol Bossa 🎗 (@oriol_bossa) March 30, 2022
La Paritat de Poder Adquisitiu
El cost de tallar-se els cabells és un bon indicador del cost de la vida en una ciutat:
Evidentemente, en Oslo llevaría el pelo más largo que lo que lo llevo aquí.
— Manuel Hidalgo (@Manuj_Hidalgo) June 28, 2020
Paridad de poder adquisitivo por ciudades en un grafico pic.twitter.com/i1xUUCIHs0
Logaritme
L’escala logarítmica s’utilitza en una variable numèrica per principalment dos motius, un d’empíric i un de teòric:
- Empíric: Per representar millor els valors de la distribució quan els valors estan concentrats en l’extrem inferior. Direm que aquest tipus de distribució té una asimetria negativa).
- Teòric: En el cas de variables com el PIB per càpita, per representar millor la diferència en els efectes que té una unitat addicional en els valors baixos i els valors alts de la distribució.
Significat empíric del logaritme
Per conèixer el significat empíric del logaritme, carregarem les llibreries tidyverse i gapminder.
library(tidyverse)
library(gapminder)El marc de dades gapminder conté informació sobre el PIB per càpita, l’esperança de vida i la població de la majoria de països del món. Bona part de les variables numèriques, com l’esperança de vida, acostumen a tenir un dibuix semblant al que veiem a la Figura 1. La majoria de les observacions estan ubicades més o menys al centre de la distribució. En canvi, hi ha algunes variables, com el PIB per càpita, que tenen una distribució asimètrica: la major part dels valors estan ubicats a un extrem de la distribució mentre que només uns pocs casos es troben a l’altre extrem. Al gràfic observem com la majoria de països es troba en valors molt baixos (penseu que hi ha dades dels anys 50 i 60, quan pràcticament tots els països eren pobres). En canvi, hi ha molts pocs valors per sobre de 30.000.
gapminder %>%
pivot_longer(c(lifeExp, gdpPercap), "vars") %>%
ggplot(aes(x = value)) +
geom_histogram(alpha = 0.4) +
facet_wrap(.~ vars, scales = "free") +
theme_bw()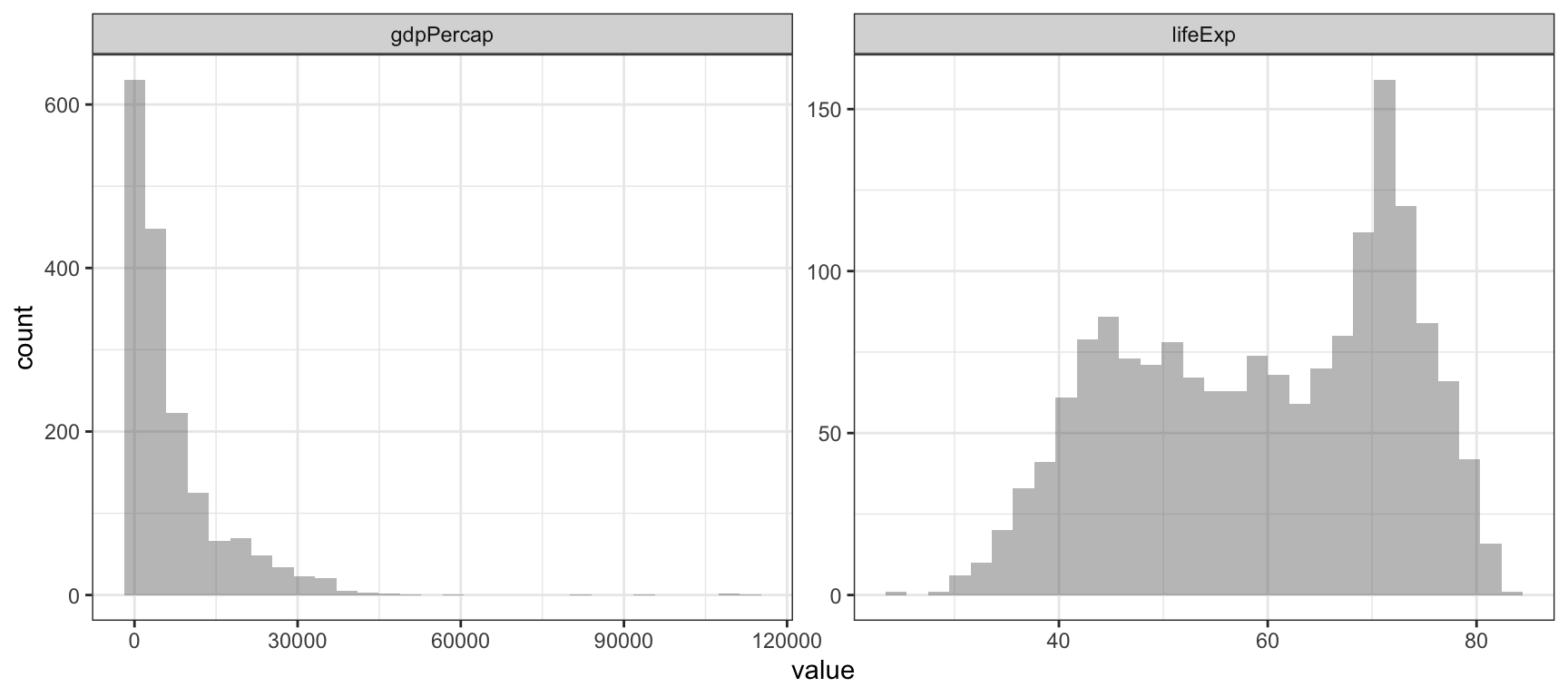
Figure 1: Distribució del PIB per càpita i l’esperança de vida mundial
Quan tenim asimetria negativa, en què la major part de les observacions estan concentrades en valors baixos, utilitzarem el logaritme per tal d’aconseguir que la variable prengui forma d’una distribució normal. Si apliquem el logaritme a les dades de PIB per càpita del gràfic anterior, obtindrem la Figura 2.
gapminder %>%
ggplot(aes(x = log10(gdpPercap))) +
geom_histogram(alpha = 0.4) +
theme_bw()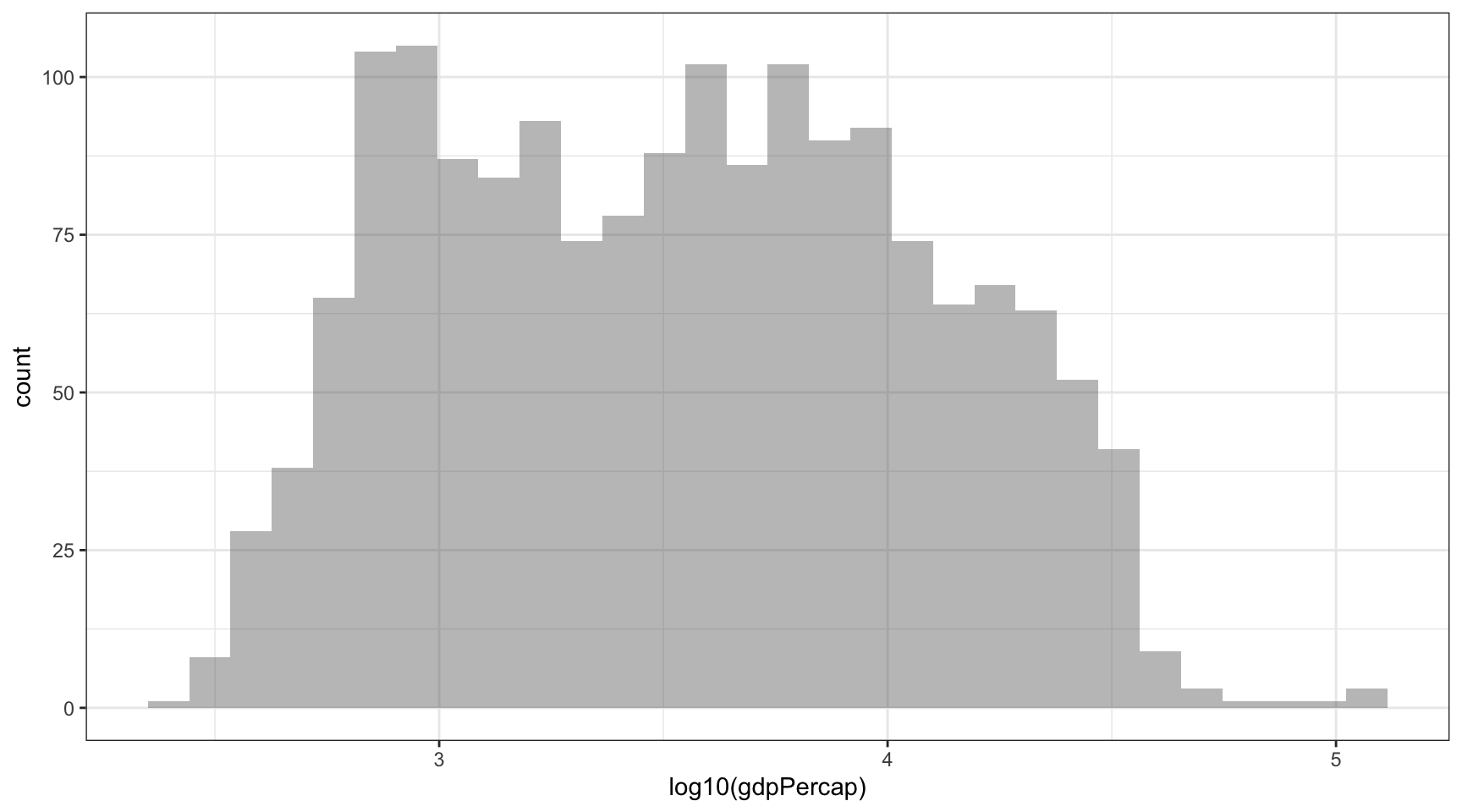
Figure 2: Distribució del PIB per càpita mundial a escala logarítmica
Amb el logaritme aconseguim modificar la forma de la distribució, de manera que podem representar més nítidament els casos que hi ha en els valors baixos. Una de les complicacions d’aplicar el logaritme és la interpretació d’aquests nous valors, però per sort interpretar el logaritme amb base 10 pot acabar resultant relativament senzill.
Exercici 1. A la Figura 2 hem aplicat el logaritme amb base 10. Busca com interpretar-lo i respon:
- Quins valors de PIB per càpita representen els números 3, 4 i 5 de l’eix horitzontal? Per què no apareix el número 2?
- En quin punt aproximat en valors de PIB per càpita tenim més casos? Podíem respondre a aquesta pregunta amb el gràfic de la Figura 1?
- Quin tipus de distribució tenim ara en aquest gràfic?
Significat teòric del logaritme
Aplicar el logaritme neperià al PIB per càpita va molt lligat a les teories utilitaristes. Hi ha un cert consens entre els economistes que els ingressos tenen efectes marginals decreixents en el benestar de les persones. És a dir, una persona pobre gaudirà molt més de 10 euros addicionals que no pas si aquests mateixos 10 euros els donem a una persona rica. L’ús del logaritme sobre el PIB per càpita reprodueix aquesta lògica, ja que emfatisarà les variacions als nivells baixos de la distribució i reduirà les variacions als nivells alts.
Ho veurem amb un exemple il·lustratiu amb el marc de dades utility, que observem a la Taula 1. A la primera columna income hi hem ubicat varis trams de renda d’una persona, començant per 500 euros i acabant amb 45.000. A la segona columna wellbeing hem creat una escala de benestar, que respon a la pregunta: quin benestar té vostè en escala de 1 a 10? Com que assumim que les dues variables creixen de forma lineal, a cada increment de nivell de renda es traduirà en un increment d’un punt a l’escala de benestar. Per exemple, si passem de guanyar 500 a guanyar 5.000 euros passarem d’un benestar 1 a un benestar 2. De la mateixa manera, si passem de 32.000 a 36.500 euros passarem de benestar 8 a benestar 9. En els dos casos, un increment en 4.500 euros suposa un increment en un punt a l’escala de benestar.
utility <- tibble(income = seq(500,45000, 4500),
wellbeing = 1:10)| income | wellbeing |
|---|---|
| 500 | 1 |
| 5000 | 2 |
| 9500 | 3 |
| 14000 | 4 |
| 18500 | 5 |
| 23000 | 6 |
| 27500 | 7 |
| 32000 | 8 |
| 36500 | 9 |
| 41000 | 10 |
Un utilitarista ens diria que la taula que acabem de construir és errònia. Un augment d’ingressos en nivells baixos de renda es tradueix en un augment molt més pronunciat en l’escala de benestar que un augment de la mateixa quantitat en nivells alts. És per això, que en la següent Figura 3 hem deformat aquesta relació. El logaritme ara representa millor la relació entre ingrés i benestar. A nivells baixos, un augment de renda es tradueix en un augment molt important del benestar. En canvi, a nivells alts, un augment de renda es tradueix en un augment molt petit en benestar.
utility %>%
mutate(wellbeing_log = log10(wellbeing)) %>%
pivot_longer(wellbeing:wellbeing_log, "vars") %>%
ggplot(aes(x = income, y = value)) +
geom_line() +
facet_wrap(.~vars, scales = "free")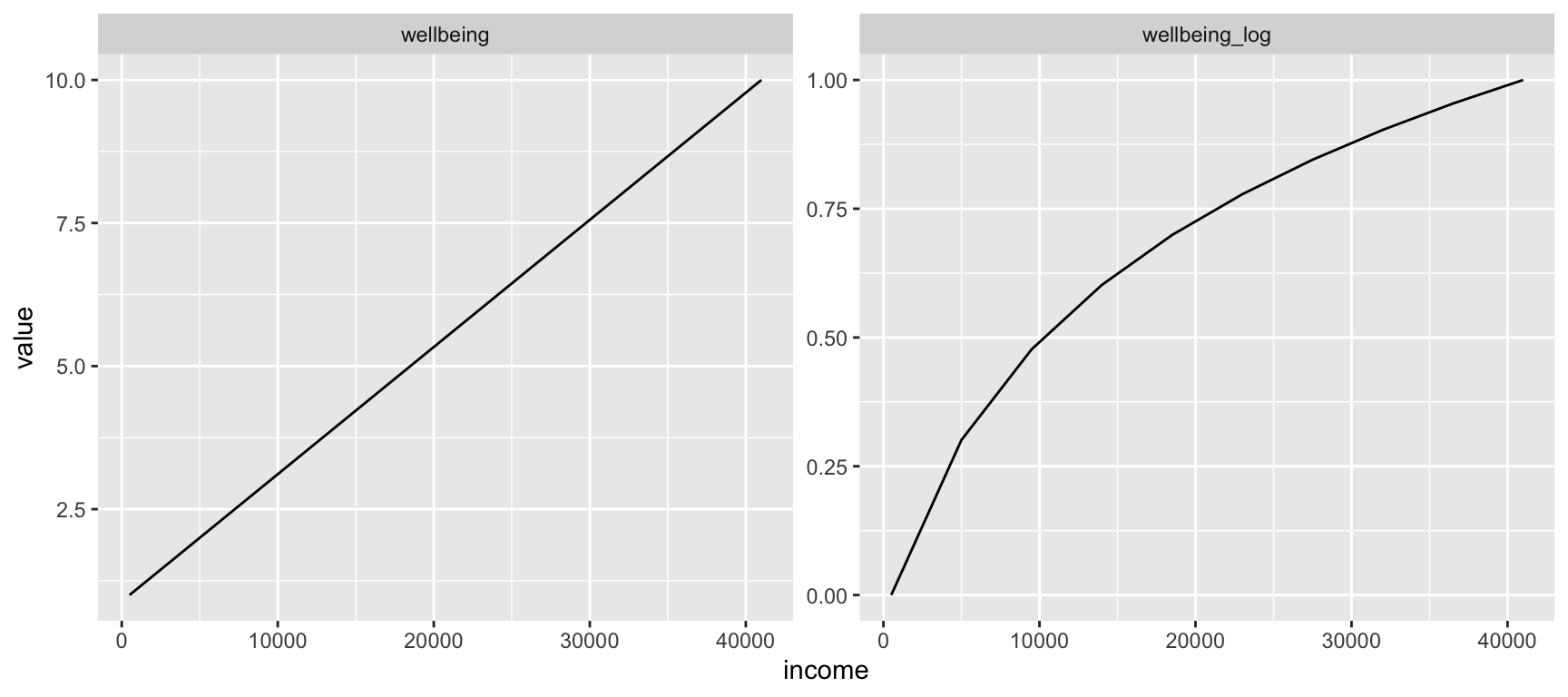
Figure 3: Relació entre renda i benestar
La relació entre renda i benestar no és lineal, com mostra el gràfic de l’esquerra. La relació pren una forma més aviat similar al gràfic de l’esquerra, on hem aplicat el logaritme amb base 10. El logaritme s’utilitza per reflectir la relació entre els ingressos i molts fenòmens socioeconòmics, com el benestar o l’esperança de vida. Sense anar més lluny, l’Índex de Desenvolupament Humà utilitza el logaritme “per reflectir els rendiments decreixents de transformar els ingressos en capacitats humanes. En altres paraules, les persones no necessiten excessius recursos financers per assegurar-se un estàndard de vida decent” (UNDP 1990, 12; veure també Haq 1999, 49).
- Més informació: The Society Pages
Big Data
El Big Data ha canviat les nostres vides. Podem utilitzar moltes dades de forma massiva gràcies a les noves tecnologies. Per exemple, podem saber moltes coses del comportament de les persones només amb una simple cerca a Google Trends. Quan han tingut més interès els escacs en els darrers anys? Podem pensar que les cerques de la paraula ‘chess’ a Google pot correspondre a l’interès pels escacs que ha tingut a la població mundial en els últims anys:
Exercici 2. Intenta, mitjançant Big Data, respondre a les següents preguntes:
- A què corresponen els pics del gràfic?
- En quin país europeu hi ha més preocupació per Síria?
- Com de popular ha estat Kamala Harris a la política americana?
- El govern d’Ecuador està pensant obrir una aerolínia i pretén establir una vol directe amb Espanya. Recomanaríeu establir una connexió amb Madrid o amb Barcelona?
- Assessoreu un polític que fa una visita al Brasil. A la festa després del meeting, posaríeu música de Metallica o de Bon Jovi?
- Com de bé servirien les paraules ‘trump’ i ‘biden’ per prediure el guanyador a cada estat nordamericà a les eleccions presidencials del 2020? I ‘republican party’ i ‘democratic party’? Se t’acudeixen dues paraules que ajudin a predir de manera més acurada el vot?